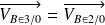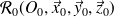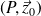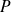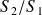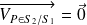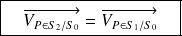C03_P2 : Cinématique Graphique - Cas du mouvement plan

Afficher le planAfficher le plan

Composition des vecteurs vitesse - Application graphique

Rappel

Soit un solide 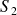auquel on associe le repère en mouvement par rapport à deux solides et 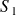auxquels on associe respectivement les repères 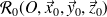et .

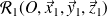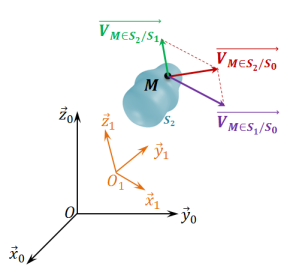
Pour tout point M appartenant au solide 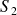, on a :

\boxed{\quad\overrightarrow{V_{M,S_2/\mathcal{R}_0}}= \overrightarrow{V_{M,S_2/\mathcal{R}_1}}+\overrightarrow{V_{M,\mathcal{R}_1/\mathcal{R}_0}} \quad }

Application graphique

MéthodeComposition des vecteurs vitesse

Soient 3 solides 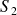, 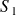et 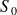en mouvements relatifs.

Connaissant :

  • un vecteur vitesse : ,

  • deux supports en un même poin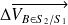t : et ,

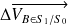on peut construire graphiquement et :

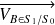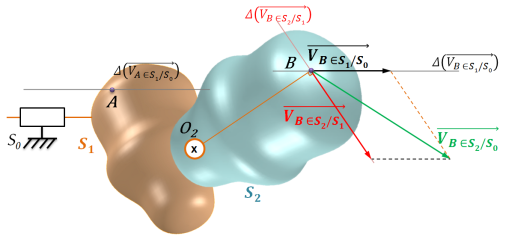
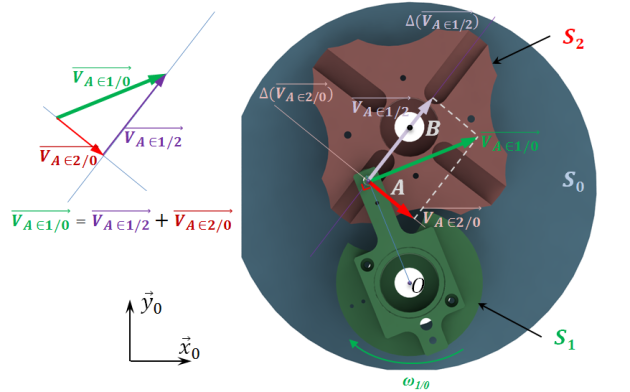
  1. Tracer le vecteur vitesse connu.

  2. Tracer les droites parallèles aux supports connus à chaque extrémités du vecteur vitesse (deux constructions possibles, donnant le même résultat) afin d'obtenir les normes des deux vecteurs vitesse recherchés.

  3. Le sens de ces vecteurs se détermine grâce à la relation de composition des vecteurs vitesse : = + .

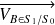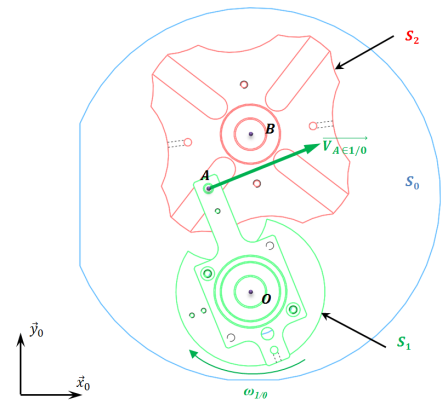
ExempleCroix de Malte

Ce mécanisme transforme le mouvement de rotation continu de l'arbre 1 en un mouvement de rotation intermittent de l'arbre 2.

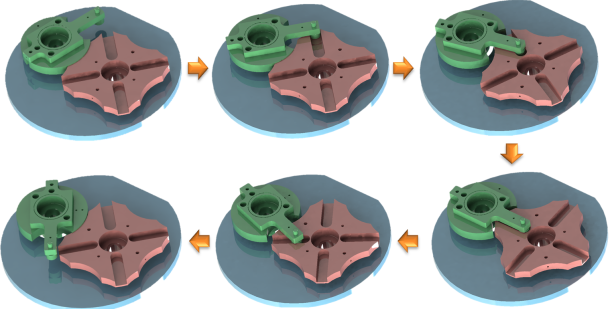
Travail demandé :

  • Le maneton 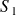est en rotation d'axe 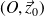par rapport au carter .

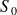  • La croix de Malte 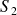est en mouvement de rotation d'axe 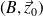par rapport au carter .

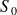  • Le mouvement de la croix de Malte 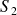par rapport au au maneton 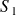est un mouvement plan sur plan de normale .

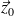  • Dans la configuration de la figure ci-dessous, on donne le vecteur vitesse .

→ Déterminer graphiquement les vecteurs vitesse 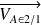et .

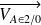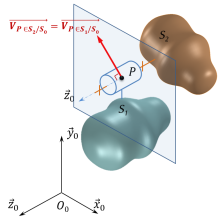
Cas particulier : composition des vitesse en un point d'un axe de rotation

Soient deux solides et en mouvement sur plan par rapport à un solide auquel on associe le repère de référence . On suppose que et sont en liaison pivot d'axe .

Appliquons la relation de composition des vecteurs vitesse au point  :

.

Or P est sur l'axe de rotation de , donc par définition d'un mouvement de rotation :

Ainsi :

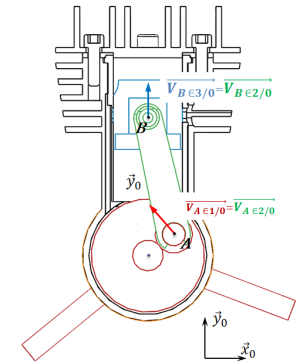
ExempleMicromoteur de modélisme

La relation de composition des vecteurs vitesse en A entre la bielle 2, la manivelle 1 et le carter 0 s'écrit :

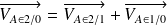
Or la bielle 2 et la manivelle 1 sont en liaison pivot d'axe 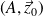donc .

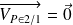Ainsi,

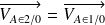
En procédant de même au point B avec le piston 3, la bielle 2 et le carter 0, on montre que :

PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimerRéalisé avec Scenari (nouvelle fenêtre)