Equiprojectivité
Théorème
Soient deux points
et
appartenant à un même solide
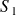en mouvement plan par rapport à un solide de référence
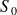auquel on associe le repère
.
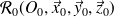Soient
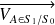et
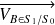les vecteurs vitesse respectifs de ces points dans le mouvement de
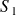par rapport à
.
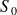La projection orthogonale de
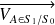sur
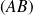est égale à la projection orthogonale de
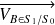sur
.
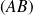Complément : Démonstration
D'après le champ des vecteurs vitesse :
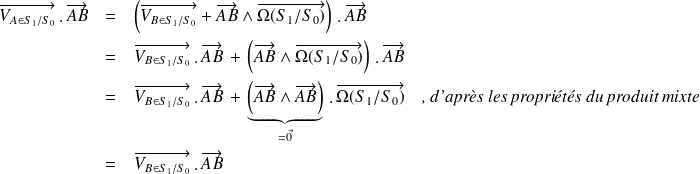
Application graphique
Méthode : Equiprojectivité
Connaissant :
le vecteur vitesse en un point
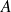de
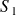en mouvement plan sur plan par rapport à
:
,
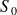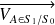le support du vecteur vitesse en autre point B :
,
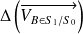on peut construire graphiquement le vecteur vitesse du point B :
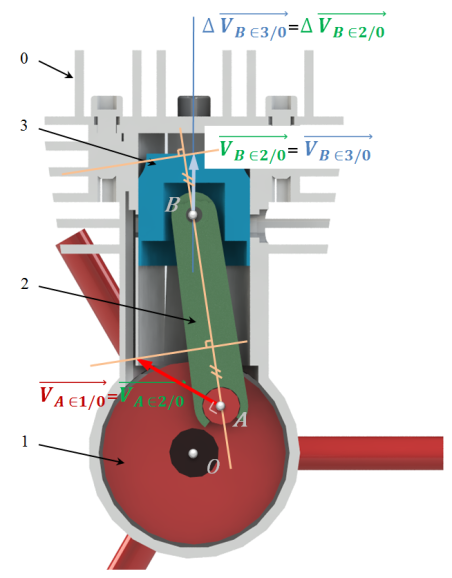
On trace la droite
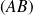.On construit la projection de
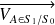sur
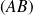.On reporte cette projection au point B, du même coté du point.
On en déduit
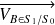car
(
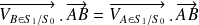
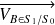a la même projection sur
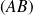que
).
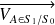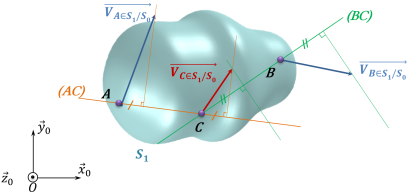
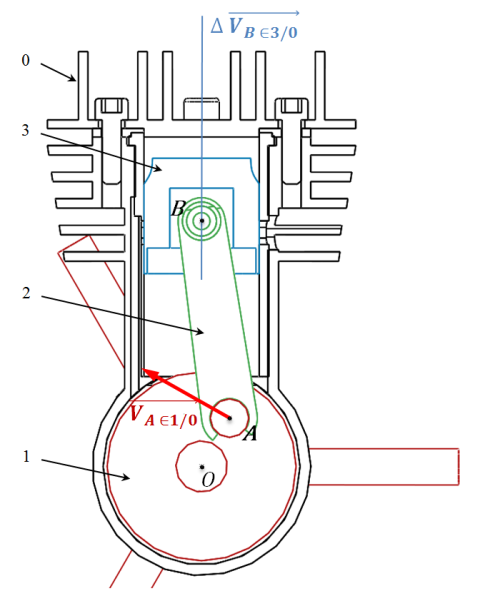
Exemple : Micromoteur de modélisme
On suppose que
,
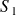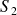et
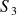ont des mouvements plans sur plans de normale
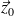par rapport au carter
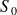. On donne
et le support
.
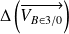→ Déterminer graphiquement
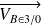en utilisant l'équiprojectivité.
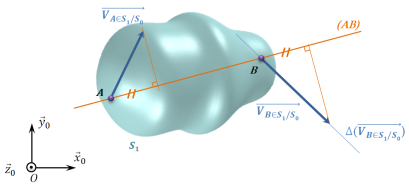
Méthode : Double équiprojectivité
Connaissant :
le vecteur vitesse en un point
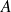de
en mouvement plan sur plan par rapport à
:
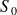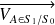,le vecteur vitesse en un autre point
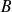de
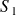par rapport à
:
,
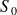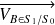on peut construire graphiquement le vecteur vitesse de n'importe quel autre point
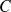du solide
:
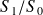On trace les droites
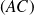et
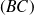.On applique deux fois l'équiprojectivité telle que décrite au paragraphe précédent :
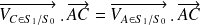et
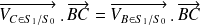
On en déduit
